Le Mode
Variable discrète:
La valeur du variable dont l'effectif maximum donne le mode.
Il peut aussi y avoir un mélange de deux populations qui conduit à un diagramme en bâtons où apparaissent deux bosses; on considérera deux modes. Il est déconseillé, sauf raison explicite, d'envisager plus de deux modes.
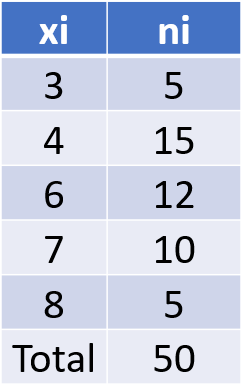
Le Mode dans ce cas est "4"
Variable classée:
la classe modale correspond à la classe ayant l'effectif maximum. Il est fortement conseillé d'utiliser l'histogramme pour déterminer le mode. Comme pour le cas discret, on peut avoir deux classes modales. Toutes les valeurs de la classe pouvant à priori se réaliser, on ne se contentera pas de déterminer la classe modale. Une des valeurs de cette classe sera le mode. Certains auteurs préconisent par simplicité de prendre le centre de la classe modale. Il est préférable cependant de tenir compte des classes adjacentes de la manière suivante:
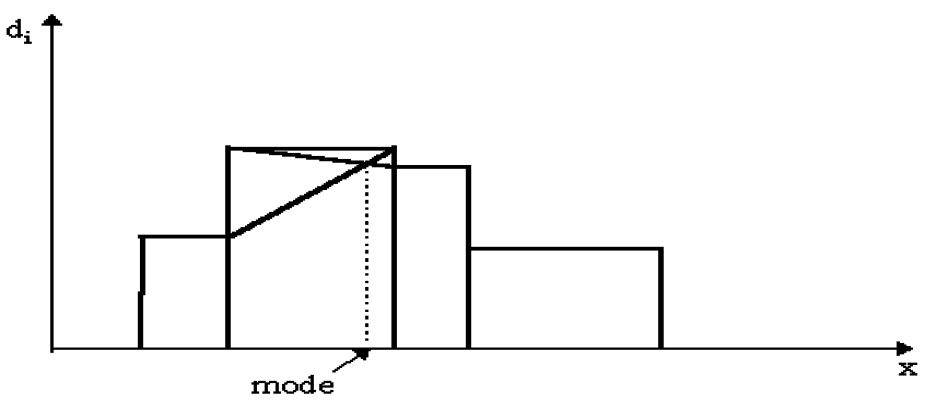
Amplitudes égaux:
La formule du Mode :
\begin{equation} \begin{aligned} Mode = Limite_{inférieur} + \left( \frac{d_{1}}{ d_{1} + d_{2} }\right) \times a \end{aligned} \end{equation}
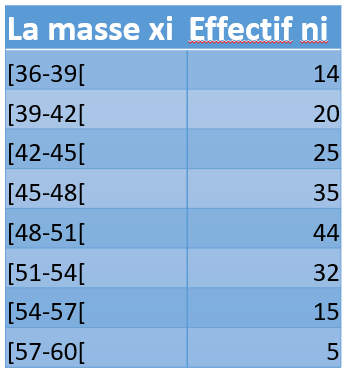
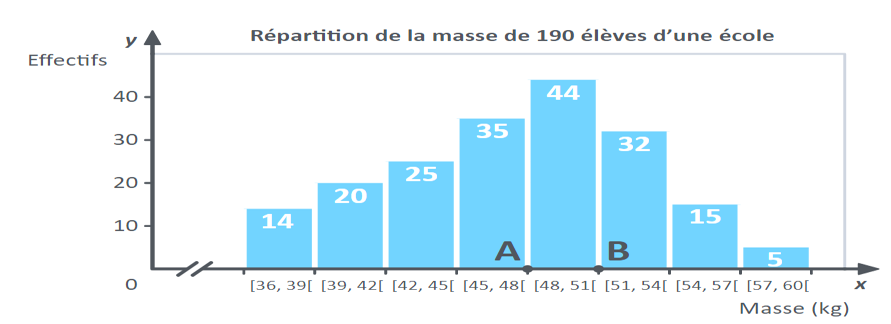
La classe modale: La classe ayant l'effectif maximum = [48-51[
Limiteinférieur: La limite inférieur de la classe modale = 48
d1: La difference entre l'effectif de la classe modale et l'effectif de la classe précédente de la classe modale = 44-35 = 9
d2: La difference entre l'effectif de la classe modale et l'effectif de la classe suivante de la classe modale = 44-32 = 12
a: l'amplitude de la classe modale = 51-48 = 3
\begin{equation} \begin{aligned} Mode = 48 + \left( \frac{9}{ 9+ 12 }\right) \times 3 \end{aligned} = 48.29 \end{equation}
Amplitudes inégaux:
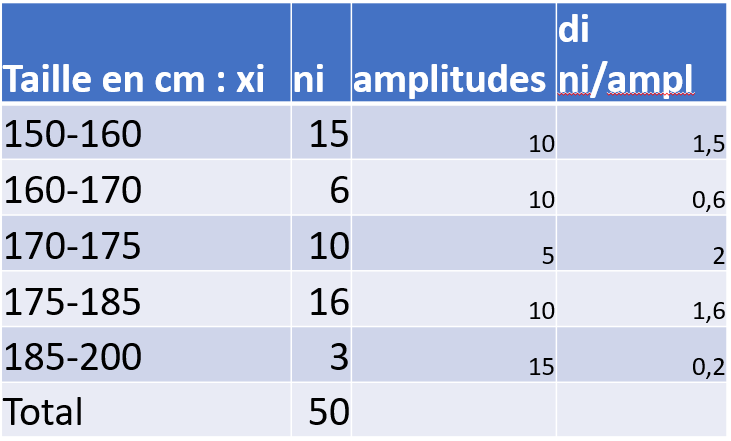
La classe modale: La classe ayant l'effectif di maximum = [170-175[
Limiteinférieur: La limite inférieur de la classe modale = 170
d1: La difference entre l'effectif de la classe modale et l'effectif de la classe précédente de la classe modale = 2-0.6= 1.4
d2: La difference entre l'effectif de la classe modale et l'effectif de la classe suivante de la classe modale = 2-1.6= 0.4
a: l'amplitude de la classe modale = 175-170 = 5
\begin{equation} \begin{aligned} Mode = 170+ \left( \frac{1.4}{ 0.4+ 1.4}\right) \times 5 \end{aligned} = 173.88 \end{equation}