Les valeurs étant rangées par ordre croissant, c'est la valeur de la variable qui sépare les observations en deux groupes d'effectifs égaux.

Médiane pour variable discrète:

la détermination peut s'obtenir à partir du tableau statistique en recherchant la valeur de la variable correspondant à une fonction cumulée égale à n/2 (effectif cumulé) ou ½ (fréquence cumulée)

Exemple:

Application1 :

Soit la série statistique impaire suivante :

23 17 20 18 13

TAF : Calculez la médiane de cette série

Eléments de réponse :

Me=18

Application2 :

Soit la série statistique paire suivante :

23 17 20 18 13 15

TAF : Calculez la médiane de cette série

Eléments de réponse :

Me=17.5

Application3 :

Soit la série statistique paire suivante :

19 17 20 18 17 17 20 19 15 16 20 23 22 14 15 24

TAF : Calculez la médiane de cette série

Eléments de réponse :

Me=18.5

Médiane pour variable classée:

l'abscisse du point d'ordonnée n/2 ( ½ pour la fréquence)se situe en general à l'intérieur d'une classe. Pour obtenir une valeur plus précise de la médiane, on procède à une interpolation linéaire. La valeur de la médiane peut être lue sur le graphique ou calculée analytiquement.

Application4 :

Calculez la médiane de cette série.

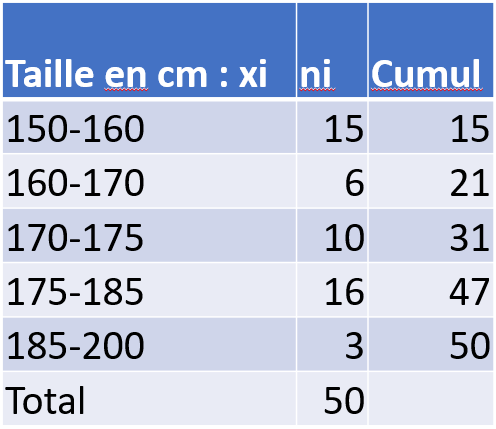
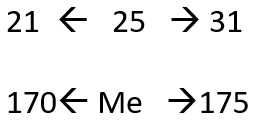
\begin{eqnarray} {\displaystyle {\frac {Me - 170}{175-170} = { \frac {25-21}{31-21} } }} \end{eqnarray}

\begin{eqnarray} {\displaystyle { Me = 172 }} \end{eqnarray}